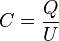Kondensator – jest to element elektryczny (elektroniczny), zbudowany z dwóch przewodników (okładek) rozdzielonych dielektrykiem.

Opis teorytyczny

Doprowadzenie napięcia do okładek kondensatora powoduje zgromadzenie się na nich ładunku elektrycznego. Po odłączeniu od źródła napięcia, ładunki utrzymują się na okładkach siłami przyciągania elektrostatycznego. Jeżeli kondensator, jako całość, nie jest naelektryzowany to cały ładunek zgromadzony na obu okładkach jest jednakowy co do wartości, ale przeciwnego znaku. Kondensator charakteryzuje pojemność określająca zdolność kondensatora do gromadzenia ładunku:

C = \frac Q U

gdzie:

C – pojemność, w faradach
Q – ładunek zgromadzony na jednej okładce, w kulombach
U – napięcie elektryczne między okładkami, w woltach.

Pojemność wyrażana jest w faradach. Jeden farad to bardzo duża jednostka, dlatego w praktyce spotyka się kondensatory o pojemnościach piko-, nano-, mikro- i milifaradów[1]. Odwrotnością pojemności elektrycznej jest elastancja wyrażana w darafach (nie jest to jednostka układu SI).

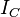Ogólnie, napięcie U_C i prąd I_C kondensatora w chwili t związane są zależnością:

U_C=\frac Q C = {1 \over C} \int_{-\infty}^t I_C(\tau) \mbox{d} \tau

Pracę dW, jaką trzeba wykonać, by przenieść niewielki ładunek dq z jednej okładki kondensatora, o pojemności C, na drugą, przy założeniu, że jedna z okładek jest naładowana ładunkiem q.

\mbox{d}W=U(q) \mbox{d}q = \frac q C \mbox{d}q

Energię zmagazynowaną w kondensatorze oblicza się przez scałkowanie powyższego wzoru, uzyskując:

W=\int_0^Q {q \over C} \mbox{d}q={1 \over 2} {Q^2 \over C}={1 \over 2} CU_C^2

przy czym Q jest ładunkiem, do którego naładowano kondensator.

Prąd elektryczny to zmiana ładunku w czasie, co można zapisać:

I_c(t)={{\mbox{d}Q} \over {\mbox{d}t}}= C {{\mbox{d}U_c} \over {\mbox{d}t}}

Kondensator podłączony do napięcia stałego, po pewnym czasie naładuje się do tego napięcia {{\mbox{d}U_C} \over {\mbox{d}t}}=0 Kondensator jest wówczas równoważny przerwie w obwodzie (I_c(t)=0). Dla prądu przemiennego przez kondensator płynie prąd określony wzorem:

U_c(t) = U_0 \sin(\omega t) \,
I_c= C {{\mbox{d}U_C} \over {\mbox{d}t}}= C U_0 \omega \cos(\omega t)

Wielkość, wiążąca prąd i napięcie na kondensatorze, nazywa się reaktancją, która jest tym mniejsza, im większa jest pojemność kondensatora i częstotliwość prądu. Kondensator charakteryzuje się tym, że (dla sygnałów sinusoidalnych) napięcie jest opóźnione w fazie względem prądu o kąt \frac{\pi}{2} (inaczej: prąd wyprzedza napięcie o kąt \frac{\pi}{2}). Z tego względu impedancja kondensatora jest liczbą zespoloną i opisana jest wzorem:

Z= \frac{1}{j \omega C} = \frac {-j}{\omega C}= \frac {-j}{2 \pi f C}

gdzie:

ω – częstość,
f – częstotliwość w hercach.
j – jednostka urojona

Reaktancja pojemnościowa wyraża się wzorem:

X_c = \frac {-1}{\omega C}= \frac {-1}{2 \pi f C}

przy czym ujemny znak jest kwestią konwencji.